Ögeler etikete göre görüntüleniyor: Karmaşık Sayının Trigonometrik Biçimi

Bu kullanıcının RSS akışına abone olun
Pazartesi, 05 Ekim 2015 15:45

Karmaşık Sayılar

Karmaşık Sayılar

Bir gerçel bir de sanal kısımdan oluşan bir nesnedir. a ve b sayıları gerçek olursa karmaşık sayılar şu biçimde gösterilirler:

z = a + \mathbf{i}b\,

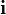Genel olarak karmaşık sayılar için "z" harfi kullanılır. \mathbf{i}^2=-1 özelliğini sağlayan sanal birime \mathbf{i} denir. Kimi zaman özellikle elektrik mühendisliğinde 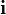\mathbf{i} yerine, \mathbf{j} kullanılır.

Ayrıca matematikte bu sayıların uzayı \mathbb{C} olarak gösterilir. Bu harfin seçilmesinin nedeni İngilizce'de karmaşık sözcüğünün karşılığı olarak complex sözcüğünün kullanılmasıdır, nitekim bazı Türkçe kaynaklarda complex sözcüğünden devşirilen komplekssözcüğüne de raslanabilir. Karmaşık sayılara böyle bir adın verilmesinin nedeni ise aşağıda da göreceğimiz gibi gerçel ve sanal kısımların bir arada durmasıdır.

Bütün gerçel sayılar sanal kısımları sıfıra eşit olan birer karmaşık sayı olarak düşünülebilir. Diğer bir deyişle gerçel sayılar, karmaşık sayı düzleminde gerçel sayılar ekseni üzerinde bulunurlar.

z = a + \mathbf{i}\cdot 0 \in \mathbb{R}

Bir z karmaşık sayısının gerçel ve sanal parçaları sırasıyla Re(z) ve Im(z) fonksiyonlarıyla gösterilir. Bütün bu tanımları ve özellikleri bir örnekte gösterelim. 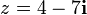z = 4 - 7\mathbf{i} sayısı gerçel kısmı Re(4-7i)=4, sanal kısmı Im(4-7i)=-7 olan \mathbb{C} uzayında bir karmaşık sayıdır.Bunun dışında karmaşık sayıların başka özellikleri de vardır. Örneğin bir karmaşık sayı düzlemde bir vektör olarak temsil edilebilir.

 

Karmaşık sayılarda cebirsel işlemler gerçel sayıların genişlemesidir. Öncelikle iki karmaşık sayının eşitliğini verelim.

Eşitlik

Bir z = a + \mathbf{i} b ve w = c + \mathbf{i} d karmaşık sayıları için

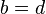z=w ancak a=c ve b=d iken geçerlidir.bu doğru bir kavramdır...

Toplama

Bir z = a + \mathbf{i} b ve w = c + \mathbf{i} d karmaşık sayıları için

z + w = ( a + \mathbf{i} b ) + ( c + \mathbf{i} d ) = ( a + c ) + \mathbf{i} ( b + d ) \,

Çarpma

Bir z = a + \mathbf{i} b ve w = c + \mathbf{i} d karmaşık sayıları için

zw = ( a + \mathbf{i} b ) ( c + \mathbf{i} d ) = ac - bd + \mathbf{i} ( bc + ad ) \,

Eşlenik

 
Bir karmaşık sayı ile eşleniğinin karmaşık uzaydaki gösterimi.

Bir z = a + \mathbf{i} b karmaşık sayısı için eşlenik ifadesi \mathbf{i} \mapsto -\mathbf{i} dönüşümüdür ve

\bar{z} = a - \mathbf{i} b

ya da matrislerde

\bar{ \mathbf{z} } = \mathbf{z}^T = \begin{bmatrix} a & b \\ -b & \;\; a \end{bmatrix}

olarak tanımlanır.

Eşleniğin cebirsel özellikleri

  • \overline {(z+w)} = \overline w + \overline z
  • \overline{ \overline z } = z
  • \overline {(zw)} = \overline w \cdot \overline z
  • \overline {(z / w)} = \overline z / \overline w
  • \overline z = z ancak z gerçel sayı olduğunda geçerlidir.

Çarpımsal ters

Bir z = a + \mathbf{i} b karmaşık sayısının tersi ancak

z^{-1} = \frac{\bar{z}}{z \bar{z}} = \frac{\bar{z}}{|z|^2} = {a\over a^2+b^2} - \mathbf{i} {b\over a^2+b^2}

olarak ya da bir matrisin tersine uygun olarak

\mathbf{z}^{-1} = { 1 \over \det \mathbf{z} } \begin{bmatrix} a & b \\ -b & \;\; a \end{bmatrix} = \begin{bmatrix} {a\over a^2+b^2} & {b\over a^2+b^2} \\ -{b\over a^2+b^2} & \;\; {a\over a^2+b^2} \end{bmatrix}

olduğu görülür.

Karmaşık sayının karekökü

\sqrt{x+i.y}=\pm \frac{1}{\sqrt{2}}\left [ \sqrt{x+\sqrt{x^2+y^2}}+\frac{i.y.\sgn(y)}{\sqrt{x+\sqrt{x^2+y^2}}} \right ]

burada \sgn(a) İşaret fonksiyonudur.

Yayınlandığı Kategori Matematik
Etiketler
Devamını okuyun...